Diffie Hellman鍵交換 をpythonで実装する

概要

1996年にDiffieとHellmanによって考案されたアルゴリズム。共通鍵暗号における鍵交換方法です。離散対数問題の困難性を利用しています。

離散対数問題とは？

離散対数問題とは、素数pと整数gが与えられて、\(y=g^x (mod p) \) の時p,g,yからxを求める問題のこと。
pが大きい場合、xを求めることが困難になる。
しかし、xが分かっていれば、yを計算することは簡単である。
x→yは容易、y→xは難しい。これは暗号技術に利用できる。

DH法アルゴリズムの手順

Xさん、Yさんが通信する

①事前準備
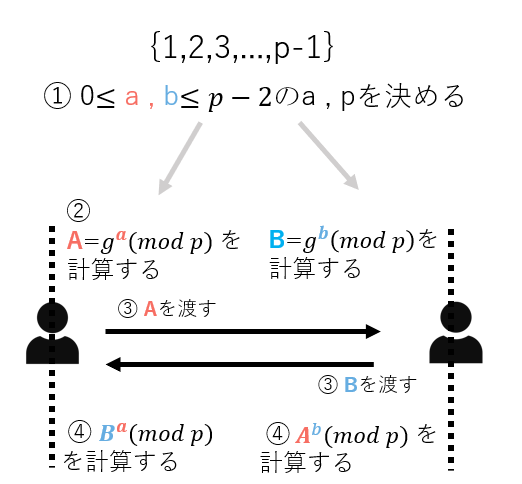
大きな素数pを決める。有限体{1,2,3,…,p-1} の生成元gを選ぶ。a、b(0<=a,b<=p-1)を生成する。

②計算する
Xは\( A=g^a(mod p)\)を計算する。Yは\( B=g^b(mod p)\)を計算する。

③相手に計算した値を送信する
XはYにAを送信する。YはXにBを送信する。

④共通鍵を求める
Xは\( B^a(mod p)\)を計算、Yは\( A^b(mod p)\)を計算する。
これは\( g^ab(mod p)\)となり同じ値となる。この値を共通鍵として利用する。

送信しているA,Bが判明しても、a,ｂを求めるのは、離散対数問題となり困難である。

Pythonで実装したコード

import random


def generate_element(num):
    """
    入力した数字の生成元を配列で返す関数
    """
    elements = []
    for i in range(1, num):
        check = sorted([i ** j % num for j in range(1, num)])
        if check == list(set(range(1, 29))):
            elements.append(i)
    return elements


def main():
    p = 29
    print(f"与えられた素数は{p}")
    # 生成元を求める関数
    elements = generate_element(p)
    print(f"生成元は{elements}")
    random_element = random.choice(elements)
    print(f"選んだ生成元は{random_element}")
    #
    a = random.randint(0, 29)
    b = random.randint(0, 29)
    print(f"選ばれたaは{a},bは{b}")

    A = (random_element ^ a) % p
    B = (random_element ^ b) % p
    print(f"割った余りAは{A}")
    print(f"割った余りBは{B}")

    Ka = (B ^ a) % p
    Kb = (A ^ b) % p
    print(f"割った余りKaは{Ka}")
    print(f"割った余りKbは{Kb}")


if __name__ == "__main__":
    main()

感想

今回は簡単に数字でやる方法について紹介しました。数字と文字、数字とデータを変換することで実用的な暗号プロトコルとして利用出来ます。

サムネ Image by Engin Akyurt from Pixabay

莉莉

今年もよろしくお願いします！！
毎週木、日 20:00に更新の『寺小屋 莉々』をよろしくお願いします！！